Research Theme

Statistics plays a pivotal role in today’s big/small data challenges. My research interests lie in developing Bayes theory and methods for a board range of statistical problems, such as high-dimensional data analysis, nonparametric problems, uncertainty quantification, and large-scale heterogeneous data problems. I also develop new Bayesian methods for various applications, including electronic health records, dynamic treatment regimens, cancer genomics, early detection of Alzheimer’s disease, mental health in people with HIV, early-phase clinical trial designs, and material engineering. Examples of previous and ongoing research conducted by the research group are listed below, including 1) Bayes theory and methods for high-dimensional data ; 2) Methods and applications to HIV related studies ; 3) Reinforcement learning and Dynamic treatment regimens for precision medicine ; 4) Bayesian early-phase clinical trial designs ; 5) Interpretable Augmented Intelligence for Material Engineering .

Bayes theory and methods for high-dimensional data

In contemporary statistics, datasets are typically collected with high-dimensionality, where the dimension can be significantly larger than the sample size. In the high-dimensional setting, additional structural assumptions are often necessary in order to address challenges associated with statistical inference. For example, sparsity is introduced for sparse covariance/precision matrix estimation, and low-rank structure is enforced in spiked covariance matrix models. Taking network data analysis as an example. Latent position graphs have been proved to be useful for varieties of network analysis problems, and we focus on a particular class of latent position graphs: the random dot product graphs. They are simple in architecture but can be used as a building block for approximating more general latent position graphs with positive definite link functions. The techniques for statistical analysis on random dot product graphs so far have been focusing on spectral methods, e.g., the adjacency spectral embedding (ASE), whereas the likelihood information is neglected. Furthermore, it remains open what is the minimax risk for estimating the latent positions, and how can one achieve it by constructing a useful estimator? The overall goal is to establish the theoretical framework of Bayesian models for random dot product graphs completely by showing both its first-order and second-order optimality.

Selected Publications:

1. Xie F⁺ , Xu Y^# , “Efficient Estimation for Random Dot Product Graphs via a One-step Procedure.” arXiv:1910.04333
2. Xie F⁺ and Xu Y^# , Carey Priebe, and Joshua Cape, “Bayesian Estimation of Sparse Spiked Covariance Matrices in High Dimensions.” arXiv:1808.07433
3. Xie F⁺ and Xu Y^# , “Optimal Bayesian Estimation for Random Dot Product Graphs.” arXiv:1904.12070 / Biometrika
   Biometrika, 2020; asaa031

Grants:

1. NSF 1940107 (Principal Investigator)

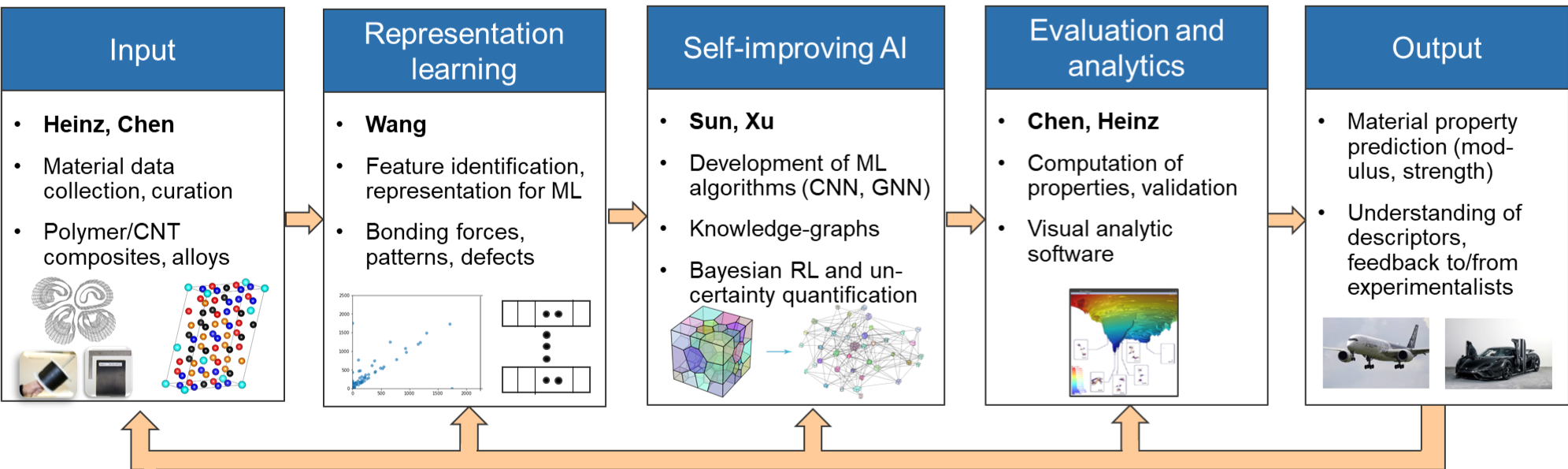
Methods and applications to HIV related studies

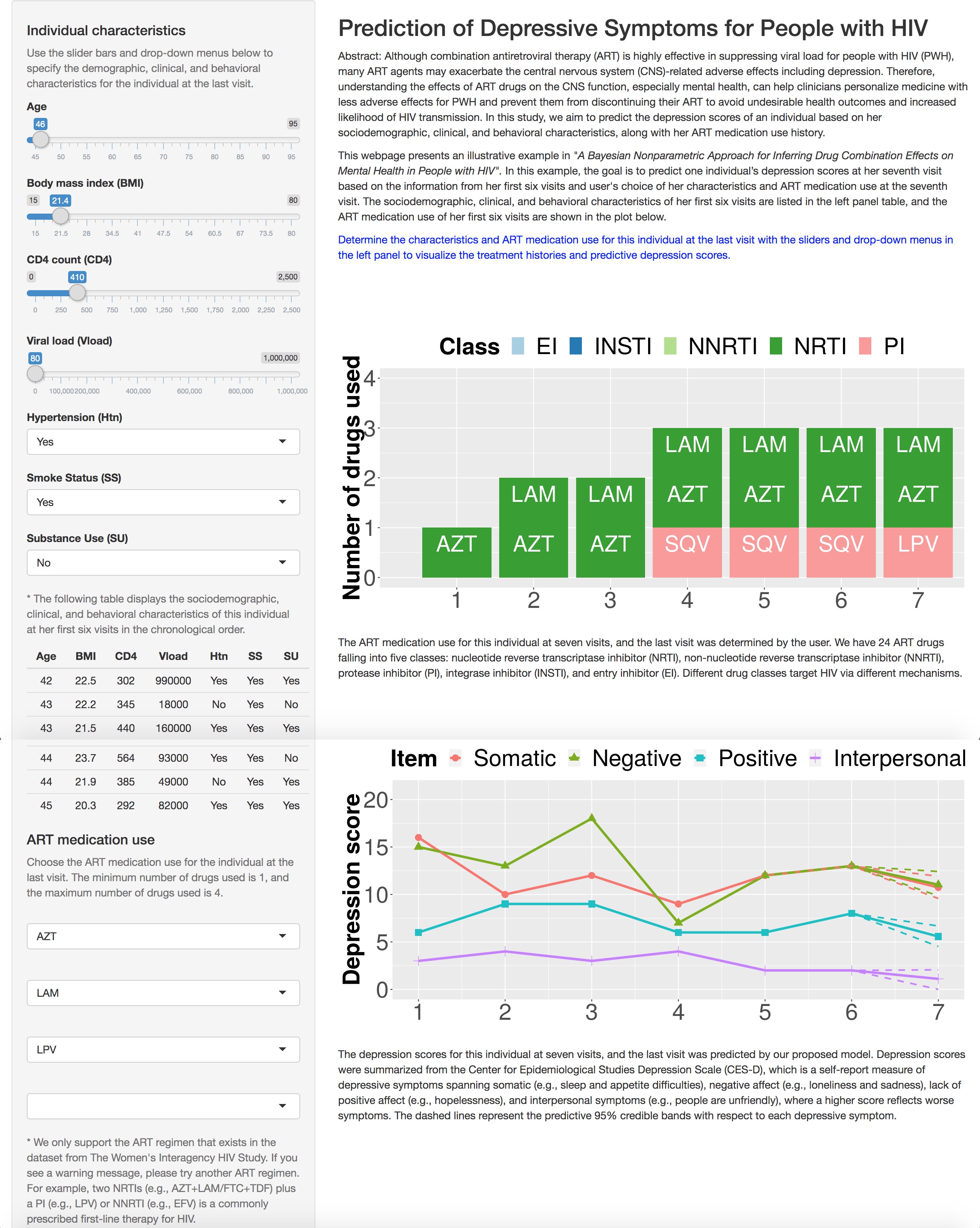
Although combination antiretroviral therapy (ART) is highly effective in suppressing viral load for people with HIV (PWH), many ART agents may exacerbate central nervous system (CNS)-related adverse effects including depression. Therefore, understanding the effects of ART drugs on the CNS function, especially mental health, can help clinicians personalize medicine with less adverse effects for PWH and prevent them from discontinuing their ART to avoid undesirable health outcomes and increased likelihood of HIV transmission. The emergence of electronic health records offers researchers unprecedented access to HIV data including individuals’ mental health records, drug prescriptions, and clinical information over time. However, modeling such data is very challenging due to high-dimensionality of the drug combination space, the individual heterogeneity, and sparseness of the observed drug combinations. We develop Bayesian approaches to learn longitudinal drug effects and drug combination effects on mental health in PWH adjusting for socio-demographic, behavioral, and clinical factors. Our method has clinical utility in guiding clinicians to prescribe more informed and effective personalized treatment based on individuals’ treatment histories and clinical characteristics.

Selected Publications:

1. Jin W⁺ , Ni Y, Rubin LH, Spence AB and Xu Y^# , “A Bayesian Nonparametric Approach for Inferring Drug Combination Effects on Mental Health in People with HIV.” arXiv:2004.05487 / RShiny
2. Asante R Kamkwalala^* , Kunbo Wang^*+ , P Jane O’Halloran, Dionna W. Williams, Raha Dastgheyb, Kathryn C. Fitzgerald, Amanda B. Spence, Pauline M. Maki, Deborah R. Gustafson, Joel Milam, Anjali Sharma, Kathleen M. Weber, Adaora A. Adimora, Igho Ofotokun, Anandi N. Sheth, Cecile D. Lahiri, Margaret A. Fischl, Deborah Konkle-Parker, Xu Y^# , Rubin LH^# , “Higher peripheral monocyte activation markers are associated with smaller frontal and temporal cortical volumes in women with HIV”.
   AIDS and Behavior, 2020.

Selected Grants:

1. NSF 1918854 (Principal Investigator)
2. The Johns Hopkins Center for AIDS Research Faculty Development Award (Principal Investigator)
3. NIH R01MH120693 (Co-Investigator)
4. NIH R01MH119947 (Co-Investigator)
5. NIH R01MH113512 (Co-Investigator)

Selected Collaborators:

1. Leah H. Rubin, Ph.D. , Johns Hopkins School of Medicine.
2. Yang Ni, Ph.D. , Texas A&M University.
3. Dionna W Williams, Ph.D. , Johns Hopkins School of Medicine.
4. Jane O’Halloran, MD , Washington University School of Medicine in St.Louis.

Reinforcement learning and Dynamic treatment regimens for precision medicine

Traditional statistical methods for dynamic treatment regimes usually focus on estimating an optimal sequence of treatments at given medical interventions, but overlook the important question of “when this intervention should happen.” This project fills in this gap by building a generative probabilistic model for a sequence of medical interventions–which are discrete events in continuous time–with a marked temporal point process where the mark is the assigned treatment or dosage. This decision model is then embedded into a Bayesian joint framework that also models clinical observations including longituindal clinical measurements and time-to-event data. We also develop a policy gradient method to train the decision model, by interacting with the observation model, to learn the personalized optimal clinical decision with the goal of optimizing patients’ health outcomes. Moreover, we have built an R package {\it doct} (short for ``Decisions Optimized in Continuous Time”) so that users can apply the proposed method to datasets in a similar setup that involves longitudinal decision making and an objective reward to optimize.

Selected Publications:

1. Hua W⁺ , Mei H, Zohar S, Giral M and Xu Y^# , “Personalized Dynamic Treatment Regimes in Continuous Time: A Bayesian Joint Model for Optimizing Clinical Decisions with Timing.” arXiv:2007.04155 / R package doct

2. Xu Y, Müller P, Wahed A and Thall P, “Bayesian Nonparametric Estimation for Dynamic Treatment Regimes with Sequential Transition Times (with discussion)”. arXiv:1405.2656 / software / supplement
   Journal of the American Statistical Association 111.515 (2016): 921-950.
   (Winner of the 2015 David P. Byar Young Investigator Travel Award Sponsored by ASA Biometrics Section)

Grants:

1. NSF 1918854 (Principal Investigator)
2. Institut National du Cancer (France), SHSESP16-031 (Co-investigator)

Bayesian early-phase clinical trial designs

Developing targeted therapies based on patients’ baseline characteristics and genomic profiles such as biomarkers has gained growing interests in recent years. Depending on patients’ clinical characteristics, the expression of specific biomarkers or their combinations, different patient subgroups could respond differently to the same treatment. An ideal design, especially at the proof of concept stage, should search for such subgroups and make dynamic adaptation as the trial goes on. When no prior knowledge is available on whether the treatment works on the all-comer population or only works on the subgroup defined by one biomarker or several biomarkers, it’s necessary to incorporate the adaptive estimation of the heterogeneous treatment effect to the decision-making at interim analyses. To address this problem, we propose an Adaptive Subgroup-Identification Enrichment Design, ASIED, to simultaneously search for predictive biomarkers, identify the subgroups with differential treatment effects, and modify study entry criteria at interim analyses when justified. More importantly, we construct robust quantitative decision-making rules for population enrichment when the interim outcomes are heterogeneous in the context of a multilevel target product profile, which defines the minimal and targeted levels of treatment effect. Through extensive simulations, the ASIED is demonstrated to achieve desirable operating characteristics and compare favorably against alternatives.

Selected Publications:

1. Xu Y^# , Constantine F⁺ , Yuan Y and Pritchett Y, “ASIED: A Bayesian Adaptive Subgroup-Identification Enrichment Design.” arXiv:1810.02285 / JBS
   Journal of Biopharmaceutical Statistics, 2020; 30(4): 623-638.
2. Xu Y, Müller P, Tsimberidou A, and Berry D, “A Nonparametric Bayesian Basket Trial Design”. arXiv:1612.02705 / BJMJ
   Biometrical Journal, 2019; 61(5): 1160-1174.
3. Xu Y, Trippa L, Müller P and Ji Y,” Subgroup-Based Adaptive (SUBA) Designs for Multi-Arm Biomarker Trial.” arXiv:1402.6962
   Statistics in Biosciences 8.1 (2016): 159-180.
   (1st Place Winner of the 2014 JSM Biopharmaceutical Section Student Paper)

Interpretable Augmented Intelligence for Material Engineering

Materials discovery and development depend on understanding and harnessing the complexity and dynamics across scales, from 3D atomic level detail to component level performance. This project will utilize recent advances in data science to understand structure-property relationships in materials and make accurate and robust property predictions. We will utilize available data more efficiently through combination with physical rules and prior knowledge to develop an interpretable augmented intelligent (AI) system to learn principles behind the association of input structures with material properties with uncertainty quantification. We have an interdisciplinary team with both domain scientists and data scientists shown below.

Grants:

1. NSF 1940107 (Principal Investigator)

Collaborators:

1. Hendrik Hain , University of Colorado, Boulder.
2. Yusu Wang , University of California, San Diego.
3. Wei Chen , Illinois Institute of Technology.
4. Steve Waiching Sun , Columbia University.