An up-to-date list of publications can be found on my Google Scholar profile and my code can be found on my Github.

My research is currently supported by ONR, NSF, The Simons Foundation, and Amazon. Previously it was supported by EOARD.

Equivariant machine learning

Equivariant machine learning refers to a class of machine learning models that respect a set of symmetries. These symmetries may arise from properties of physical law (such as conservation laws) or from redundancies in the options to mathematically represent certain objects (such as in graph neural networks). In equivariant machine learning we use group theory, invariant theory and representation theory to parameterize and study machine learning models.

    • S. Villar, D.W Hogg, K. Storey-Fisher, W. Yao, B. Blum-Smith. Scalars are universal: Equivariant machine learning, structured like classical physics. Advances in Neural Information Processing Systems (NeurIPS), vol 34, pp.28848-28863, 2021.
    • S. Villar, W. Yao, D.W. Hogg, B. Blum-Smith, B. Dumitrascu. Dimensionless machine learning: Imposing exact units equivariance. arXiv:2204.00887.
    • B. Blum-Smith, S.Villar. Equivariant maps from invariant functions. arXiv:2209.14991.

Graph neural networks

GNNs are neural network architectures which are designed to learn functions on graphs while satisfying certain symmetries (like invariance or equivariance with respect to permutations and other group actions). Part of my research studies the expressive power of these symmetry-preserving classes of functions. I’m also interested in using graph neural networks to solve combinatorial optimization problems.

  • A short tutorial on the Weisfeiler-Lehman test and its variants, N. Huang, S. Villar, IEEE International Conference on Acoustics, Speech and Signal Processing ICASSP 2021.
  • Can Graph Neural Networks Count Substructures?, Z. Chen, L. Chen, S. Villar and J. Bruna,  Advances in Neural Information Processing Systems (NeurIPS), 10383–10395, vol 33. 2020.
  • On the equivalence between graph isomorphism testing and function approximation with GNNs, Z. Chen, S. Villar, L. Chen and J. Bruna, Advances in Neural Information Processing Systems (NeurIPS), 15894-15902, 2019.
  • Revised Note on Learning Algorithms for Quadratic Assignment with Graph Neural Networks, A. Nowak, S. Villar, A. S. Bandeira and J. Bruna, In 2018 IEEE Data Science Workshop, DSW 2018, Lausanne, Switzerland: 229-233, 2018 .
  • Experimental performance of graph neural networks on random instances of max-cut, W. Yao , A. S. Bandeira and S. Villar, Wavelets and Sparsity XVIII, vol. 11138, p. 111380S. International Society for Optics and Photonics, 2019.
Clustering

Clustering is a fundamental tool for data science. It is typically formulated as an NP-hard optimization problem (like k-means), but many algorithms are quite successful in practice. In this line of research we ask the question: what are the properties of the data that make the algorithms work? We study convex and non-convex relaxations and of k-means and k-medians clustering. And we proposed algorithms that provide a data-driven probabilistic lower bound of how suboptimal a given clustering may be.

  • Probably certifiably correct k-means clustering, T. Iguchi, D. G. Mixon, J. Peterson and S. Villar, Mathematical Programming, 165(2):605–642, 2017.
  • Clustering subgaussian mixtures by semidefinite programming, D. G. Mixon, S. Villar and R. Ward, Information and Inference: A Journal of the IMA, 6(4):389–415, 2017
  • Manifold optimization for k-means clustering, T. Carson, D. Mixon, S. Villar and R. Ward, In 2017 International Conference on Sampling Theory and Applications (SampTA), pages 73–77. IEEE, 2017.
  • Relax, no need to round: Integrality of clustering formulations, P. Awasthi, A. S. Bandeira, M. Charikar, R. Krishnaswamy, S. Villar and R. Ward, In Proceedings of the 2015 Conference on Innovations in Theoretical Computer Science, pages 191–200. ACM, 2015.
  • Monte Carlo approximation certificates for k-means clustering, D. G. Mixon, S. Villar, ArXiv:1710.00956.
Dimensionality reduction and genetic marker selection

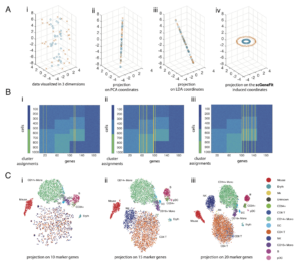
  • SqueezeFit: label-aware dimensionality reduction, C. McWhirter, D. G. Mixon and S. Villar, IEEE Transactions on Information Theory 66 (6), 3878-3892, 2019.
  • Optimal marker gene selection for cell type discrimination in single cell analyses, B. Dumitrascu, S. Villar, D. G. Mixon and B. E. Engelhardt, Nature Communications (to appear).
Matching datasets: graphs, manifolds, genetic sequences (batch correction)
  • MREC: a fast and versatile framework for aligning and matching point clouds with applications to single cell molecular data, A. J. Blumberg, M .Carriere, M. A. Mandell, R. Rabadan and S. Villar, arXiv:2001.01666
  • Revised Note on Learning Algorithms for Quadratic Assignment with Graph Neural Networks, A. Nowak, S. Villar, A. S. Bandeira and J. Bruna, In 2018 IEEE Data Science Workshop, DSW 2018, Lausanne, Switzerland,: 229-233, 2018 .
  • Efficient Belief Propagation for Graph Matching, E. Onaran, S. Villar, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 9060-9064, 2020.
  • Projected power iteration for network alignment, E. Onaran and S. Villar, In Wavelets and Sparsity XVII, volume 10394, pages 103941C. International Society for Optics and Photonics, 2017.
  • A polynomial-time relaxation of the Gromov-Hausdorff distance, S. Villar, A. S. Bandeira, A. J. Blumberg and R. Ward, ArXiv:1610.05214.
Fair redistricting and gerrymandering
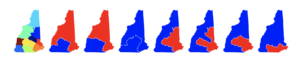  • Fair redistricting is hard, R. Kueng, D. G. Mixon and S. Villar, Theoretical Computer Science 791, 28-35, 2019.
  • Utility Ghost: Gamified redistricting with partisan symmetry, D. G. Mixon and S. Villar, ArXiv:1812.07377.