Sound Waves
Sound is the rapid cycling between compression and rarefaction of air. The way that sounds move through the air can be thought of as analogous to the way vibrations move along a slinky. Here is a link to a video in YouTube that provides a nice illustration: Slinky
The metal parts of the slinky don’t move from one end to the other. What does move along the slinky as it vibrates, is the regions where the spring is compressed or stretched out. The same thing happens when air is compressed for an instant. The air molecules themselves do not move very far, but wave of high density air moves at the speed of sound, roughly 770 miles per hour.
To represent such cyclic behavior mathematically, think of the air pressure at a listener’s location as a function of time described by a sine wave or sinusoid.
For example, a sinusoid at 440 Hz (440 cycles per second) sounds like this
Despite the fact that the sound associated with a sinusoid is not terribly pleasant to listen to, one can use such signals as basic building blocks for some truly interesting forms of sound. So it is essential to understand these key building blocks and how they combine to form complex sounds.
A sinusoid has a specific functional form that is described using the trigonometric cosine function, and we can write the most general sinusoid as the function
\(
A \sin(2\pi (ft+\phi))
\)
Here \(A\) describes the sinusoid’s amplitude which corresponds to volume, \(f\) defines its frequency, which defines its pitch, and \(\phi\) defines its phase, that is, where in a cycle, as a fraction of the whole circle, the sinusoid starts at time \(t=0.\)
A sinusoid can be thought of in geometrical terms as follows. Imagine a point moving counter-clockwise around the unit circle at a constant speed.
[KGVID]https://www.ams.jhu.edu/dan-mathofmusic/wp-content/uploads/2016/04/sinusoid2.avi[/KGVID]
The speed at which the point rotates about the orign can be measured in terms of the number of complete cycles made per second. This quantity is referred to as the sinusoid’s frequency. At each moment in time, the Cartesian coordinates \((x,y)\) of the point can be recorded, and we can plot either the \(x\) or \(y\) coordinate as a function of time. The result is shown in the bottom portion of the figure. Assuming that the point has moved by an angle \(\theta\) from the point \((1,0)\) on the \(x\)-axis, we call its \(y\)-coordinate the sine of the angle \(\theta\), denoted by \(\sin(\theta)\) and we call its \(x\)-coordinate the cosine of \(\theta\), denoted by \(\cos(\theta).\)
We assume our circle has a radius of 1 unit, making the circumference \(2\pi\). If our point starts at \((1,0)\) at time \(t=0\) and moves at a speed of \(f\) full cycles of the circle per time unit (i.e. moves a distance \(2\pi f\) per second), then in Cartesian coordinates, the position at time \(t\) is given by
\(
(\cos(2\pi ft), \sin(2\pi ft)
\)
we can represent the \(x\)-coordinate of the position at any future time \(t\) by the formula \(\cos(2\pi ft).\) On the other hand, the formula \(\sin(2\pi ft)\) defines the \(y\)-coordinate of the position at a future time \(t\) which is the \(x\)-coordinate phase-shifted by a quarter of a cycle i.e. \(\pi/2.\)
We can create the sound of a sinusoid with a given amplitude and frequency using a synthesizer and when we have two synthesizers we playing together, the result is the sum of two function formed by summing two functions. Using basic trigonometric identities, the basic sinusoid above can be expressed as a superposition of two different sinusoids
\(
A \sin(2\pi (ft+\phi)) = A_1 \sin(2\pi ft) + A_2\sin(2\pi (ft+1/4))
\)
where \(A_1 = A \cos(2\pi \phi)\) and \(A_2 = A \sin(2\pi \phi)\). So we see that it is possible for two sinusoids with the same frequency and different amplitudes and at different phases can combine to form a single sinusoid at the same frequency with some new amplitude and phase.
More generally, what happens when we play two sinusoids of given amplitudes and phases but the same frequency simultaneously? When we combine the sinusoid \(A_1 \sin(2\pi (ft + \phi_1))\) and \(A_2 \sin(2\pi (ft + \phi_2))\) to produce
\(
A_1 \cos(2\pi (ft + \phi_1)) + A_2 \cos(2\pi (ft + \phi_2))
\)
we can use some standard trigonometric identities to write this as
\(
A \sin(2\pi (ft + \phi)),
\)
for some appropriate choice of \(A\) and \(\phi\). So two sinusoids at different phases end up producing the effect of a single sinusoid.
For example, here are two sinusoids at the same frequency but with different amplitudes and phases.
[KGVID]https://www.ams.jhu.edu/dan-mathofmusic/wp-content/uploads/2016/04/two_sinusoids_same_freq.avi[/KGVID]
and when we add up these two signals we get this appearance
[KGVID]https://www.ams.jhu.edu/dan-mathofmusic/wp-content/uploads/2016/04/two_sinusdoids_same_freq_addded.avi[/KGVID]
What happens when we play two sinusoids of different frequencies and different amplitudes simultaneously? Here are plots of two different sinusoids shown separately
[KGVID]https://www.ams.jhu.edu/dan-mathofmusic/wp-content/uploads/2016/04/sinmovie1.avi[/KGVID]
When these are combined, the result is combination of waves that, when plotted, looks like this
[KGVID]https://www.ams.jhu.edu/dan-mathofmusic/wp-content/uploads/2016/04/sinmovie2.avi[/KGVID]
When we listen to music, our ears are consistently hearing combinations of sounds at various frequencies. Here’s a musical snippet from the Stone Hill All-Stars’ Miles Below the Surface
and this is what the related sound waves look like for a period of about 6/100 of a seconds.
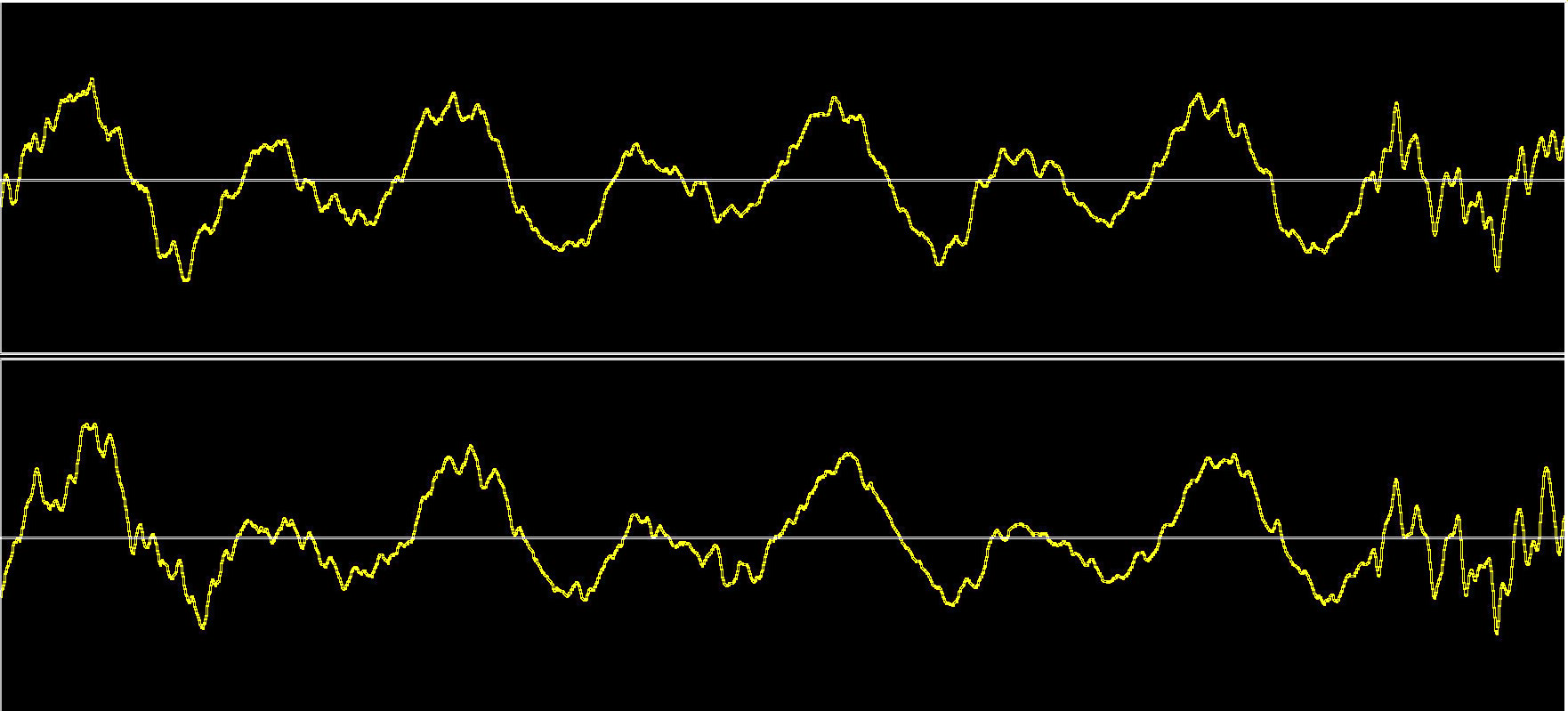
This is a stereo recording, so there are two plots displayed, one for each channel.
When sound waves are combined, the results can be quite complicated, yet, our ears are able to disentangle some sound components and hear them as separate units. When modeling what is happening mathematically, we are led one of the fundamental algebraic structures in mathematics, namely, that of a vector space. Signals/waves can be viewed as objects in what is referred to as a vector space, and such a space is equipped with two very important operations involving its objects: objects can be added together resulting in which is referred to as linear superposition, and an object can be multiplied by a number, which, in the context of sound waves would correspond to changing a sound’s volume. When we superimpose sinusoids whose frequencies are integer multiples of one another we produce sounds that are closer to what is produced by a typical musical instrument.
Vector spaces are natural structures in which to view sounds waves as superimposed simple elements, and in this framework, we can formalize some important questions:
- What are the sound waves that can be expressed as superpositions of sinusoids?
- How well can we approximate a sound wave as such a superposition?
- Given a sound wave that is sampled at regular intervals, to what extent can we recover it?
Another commonly used operation on a sound that produces a new one is amplitude modulation. For example, instead of using a sinusoid at a constant volume, we can make its volume increase rapidly to a maximum and drop off slowly to produce something more like a piano sound
