Intervals, Exponents, Logarithms
As every musician knows, musical notes have relationships with one another. The various octaves of a given note, say \(C\), sound similar to one another.
As it turns out, this is explained by the fact that the frequency associated with the octave above a note is doubled. So, for example, middle \(C\) (referred to as \(C_4\) ) has a frequency of 261.6 Hz, that is 261.6 cycles per second, while the \(C\) that is one octave higher (\(C_5\)) has a frequency that is twice that, i.e. 523.2 Hz.
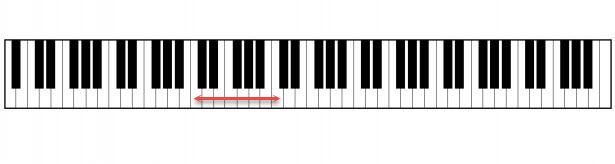
The same pattern holds for any pair of notes separated by an octave. For an interval of the same physical keyboard length, for example, as shown here
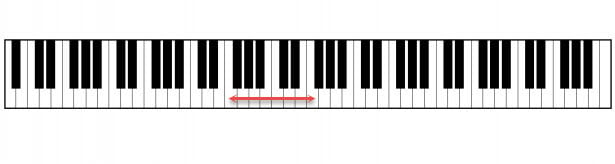
the frequency of the higher note is twice that of the lower note.
More generally, if we choose an interval of any keyboard length the higher note has a frequency that is some fixed multiple of the lower note. For example, take the interval from \(C\) to the next \(G\) on the piano as shown here
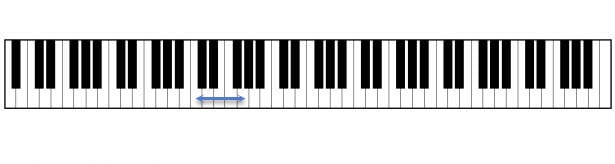
When we move from \(C\) to the next \(G\) we multiply the frequency by a factor of about 3/2, so the \(G\) above middle \(C\) has a frequency of 392.4 Hz. Similarly, if we move from \(A\) to E, the physical length of our interval is still a fifth, and the frequency of that \(E\) note is the frequency of the \(A\) multiplied by about 3/2. So we see that if we view the piano notes as ticks on a ruler, the tick distance between notes, as measured by the number of half steps separating them) translates into fixed frequency ratios. In mathematical terms, this is best explained by introducing exponents. If we pick two piano notes separated by a half-step, e.g. \(C\) to \(C\#\), and let \(\omega_0\) denote the frequency of the lower note, and \(\omega_1\) the frequency of the higher note, we have
\(
\omega_1=c\times \omega_0
\)
for some constant \(c\). But then going up an additional half step the half-note increase corresponds multiplying the frequency by this same factor of \(c\), so this whole step would have a frequency of
\(c\times c \times \omega_0 = c^2 \times \omega_0.\)
Continuing for an additional 10 half-steps, the frequency of the note we reach after 12 half-steps above the starting note will be
\(
c^12\times \omega_0
\)
But this note is an octave above the first note, so we see that
\(
c^12 \times \omega_0 = 2 \omega_0
\)
which implies that \(c\) is the 12\(^{th}\) root of 2.which implies that
\(
c = 2^{1/12} \approx 1.059463,
\)
So moving up a half-step corresponds to multiplying a note’s frequency by a factor of about 1.059463. Importantly, the note scale is an additive one: we speak of moving up by a certain number of half-steps. On the other hand, at the frequency level, this change is multiplicative. The process of going from an additive measure of length to a multiplicative one leads us to what is arguably the most important function in all of mathematics, the exponential function and its inverse the logarithm function.
Beyond describing in a clear way how to transition from notes to frequencies, these functions are important in a variety of ways for dealing with sound. For example, when we talk about loudness of a sound we use the decibels measure, whose understanding requires the logarithmic function. In addition, the complex version of the exponential function is useful for representing the sinusoidal functions and for understanding their basic properties, especially in light of one of the most beautiful and important equations in all of mathematics, namely, Euler’s identity
\(
e^{\pi i} +1 = 0.
\)
an extraordinary equation that is simple and 5 of the most important constants in mathematics.
The topic of intervals in music leads to some interesting elementary number-theoretic questions. Starting at a given note, say \(C\), suppose we play \(D\#\), a note that is 3 half-steps higher, then \(F\#\) which is again 3 half-steps higher, then another 3 half-steps to \(A\), and finally after 3 more half-steps we end up at a \(C\) again.
Starting from \(C\) and taking 3 half-steps at a time, we end up at \(C\) again on the fourth note. For other intervals, how many steps does it take to end up back at \(C\) again? For example, if each note is a single half-step higher than the previous one, we return to the note started on (an octave higher) in 12 steps.
If our interval is a fifth (7 half-steps) we have the familiar cycle of fifths
which sounds like this if we play all of the notes in the same octave
If we pick any particular interval length, how many steps does it take to end up at the note we started on? How many different possible sequence lengths can we get when each interval between successive steps is the same size? While the number 12 is a standard, we don’t have to break up an octave into 12 equal-sized steps. For example, we could use 16 steps, making the sequence of notes in an octave sound something like this
If we start at middle \(C\) and move up our modified scale in steps of 3 notes at a time until we reach another C, we end up with a sequence of 17 notes that sounds like this
Or, if we use steps of size 5, we get this
We can ask the same questions above about the note sequences formed using equal sized intervals based on this new decomposition of the octave into 16 notes. Given an interval length how can we calculate how many notes we need to play before we ended up at the note we started on? What are the possible lengths of note sequences we can obtain in this manner? What if we break up the octave into other possible numbers of pieces? These questions can be answered using a little bit of number theory. Of course to a musician it is interesting to wonder whether any of these sequences of notes sound interesting or could be used in composition.
